一、初一几何经常会出现什么样的题型?
初一学习几何分为三部分,分别是初步几何图形(点、线和角)、相交与平行线、三角形。
1、初步几何图形
(1)几何图形的概念类题型
示例:
1、下列各组图形中都是平面图形的是()。
A. 三角形、圆、球、圆锥
B. 点、线段、棱锥、棱柱
C. 角、三角形、正方形、圆
D. 点、角、线段、长方体
(2)平面与立体图形的相互转换类题型
示例:
1. 下列图形中,不可以作为一个正方体的展开图的是()。

(3)线段的计算与证明类题型
示例:
1.如下图所示,B、C是线段AD上的两点,且![]() ,求线段AD的长。
,求线段AD的长。
![]()
2. 如下图,已知数轴上点A表示数为8,B为数轴上的一点,且AB=14,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒。若M为AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否会发生变化?若变化,请说明理由;若不变,请画出图形,并求出线段MN的长。
![]()
(4)角的计算类题型
示例:
1、用A、B、C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25°,小红家在小明家正东,小红家在学校北偏东35°,则∠ACB等于()。

2、相交线与平行线
(1)概念类题型
示例:
1. 下列图形中∠1与∠2互为顶角的是()

此类题型中还包含邻角的概念(如识别邻角),垂线的概念
(2)求角类题型
示例:
1. 如下图,直线A∥ B,假设∠2=55°,∠3=100°,那么∠1的度数是()。

* 三线八角的判断是一个重点,也是一个难点,牢记同位角、内错角、同旁内角的概念是识别判断的关键。平行线的性质概括来说,两条直线平行则同位角、内错角相等,同旁内角互补。
(3)求距离类题型
示例:
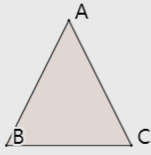
1. 如下图,在三角形ABC中有一点D在AC上移动,若AB=AC=BC=5,则AD+BD+CD的最小值是()。
(4)垂线或平行线的判定和证明类题型
示例:
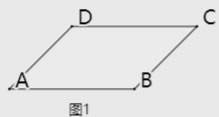
1. 如图1,已知AD∥BC,∠B=∠D。
(1)求证:AB ∥CD;
(2)若∠B=100°,点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图2,求∠FAC的度数。

二、初一几何出各种题型的目的是什么?
1、几何图形
认识几何图形
几何约占整个初中数学的40%, 几何成绩在某种意义上往往决定着整个数学考试的成败,中考也是如此,以至于有人说“得几何者得数学天下”!
几何注重理性逻辑思维,对培养学生的空间想象能力、形式思维能力及抽象思维能力十分重要,几何学好了,有助于数学其它章节甚至其它学科的学习。
事实上,几何不仅对初中数学十分重要,对孩子在高中、大学阶段的学习也很重要,即使在工作、生活中都有广泛的应用。所以,学好几何对每个孩子都很重要。
掌握知识要点
认识平面图形、立体图形。直线、射线、线段、角等概念
2、相交与平行
掌握知识要点
相交线,垂线,平行线及其判定,平行线的性质,平移。
落实数学思想
(1) 转化思想:在数学里,把一个对象转化为另一个对象,常常可以化繁为简,化未知为己知,从而达到解决问题的目的。
(2) 图形变换的思想:在平移知识中有所体现。
(3) 数形结合的思想:在几何教学中这一思想无处不在。
(4) 方程的思想:利用未知数表示有关的量,列出方程,通过解方程来求出问题的解。是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便。
(5) 构造思想:当遇到的几何问题直接解决比较困难时,可通过对图形添加辅助线来解决。
进行技能训练
(1) 推理能力的训练:由说点儿理到说理再到简单推理,最终学会用符号来表示推理过程。
(2) 画图能力的训练:本章的性质公理定理多是通过画图操作得出的,如平移中就有通过画出雪人来找到对应点连线的数量和位置关系。
(3) 几何语言的训练:教科书在通过说理的方式得出了对顶角相等的性质的基础上,进一步把这个过程写成了因为…所以…的形式;把利用垂直的定义判断角的关系的推理过程写成了因为…所以…的形式;后面的在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条的过程中,采用严格的证明形式等等,这样安排就是为了让学生逐步养成言之有据的习惯,并逐步学会用符号语言表达推理过程。
(4) 文字语言符号语言图形语言相互转化的训练:除了刚才说到的公理定理这种文字语言要用符号语言来表示之外,我们让学生画图的过程就是把文字语言转化为图形语言,同样也可以适当练习给学生图形让学生能够用语言表述图形的意思,这也为辅助线作法的叙述做了铺垫。
三、初一几何各个题型的答题方法和技巧
1、几何图形
①平面图形与立体图形的相互转化;
案例:
1. 下列图形中,不可以作为一个正方体的展开图的是()。

观察:注意审题,是“不可以”作为正方体的展开图。可以使用“一行不能多于4,7田凹应弃之”的口诀来观察。
思考:正方体沿不同棱展开可以总结为11种情况:

我们可以看出只有C不属于11种情况的任何一种,所以选C。
2. 如下图,是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是()。

观察:此题考察的是立体几何从不同方向看。先单独观察三幅各个方向的视图,再两两联合观察。
思考:单独观察:从主视图和左视图来看,知道小立方块搭成的几何体有两层,那根据俯视图来看,不管第二层有几个小立方块,第一层很明显有6个小立方块。联合观察:主视图和左视图联合起来,第二层的小立方块应该有两个,分别是中间一行的右边两个。所以小立方块的个数为8个。
②线段的计算与证明;
案例:
1. 如下图,点E,F分别是线段AC,BC的中点,若EF=3cm,求线段AB的长。
![]()
观察:仔细审题,并标记每一个条件,如E,F分别是线段AC,BC的中点,那么![]() 。
。
思考:根据观察并标记出的已知条件,![]() ,答案显而易见,写出计算过程。
,答案显而易见,写出计算过程。
计算:
解:
![]()
![]()
![]()
![]()
答:线段AB的长为6厘米。
③角的计算;
案例:
如图1,∠AOB=120°,∠COE=60°,OF平分∠AOE


(1)若∠COF=20°,则∠BOE=();
(2)如图2,求∠BOE和∠COF的数量关系;
(3)在(2)的条件下,在∠BOE内部是否存在射线OD,使∠DOF=3∠DOE,且∠BOD=70°?若存在,求∠DOF:∠COF的值,若不存在,请说明理由。
观察:注意审题,把已知条件标记出来。
思考:(1)运用逆向思维方法,要求∠BOE,那么可以从图1中可以看出可以使用已知的∠AOB-∠AOE,但∠AOE不知道,但可以使用已知条件推出,∠AOE=2∠FOE,∠FOE=∠COE-∠COF,可见(1)的结果已出。
(2)通过观察∠BOE=∠AOB(已知)-∠AOE,∠COF=∠COE(已知)-∠FOE,而∠AOE与∠FOE的关系根据已知条件OF平分∠AOE可以得出。
(3)利用方程思维,把∠DOE设为x,那么∠DOF为3x,∠AOF=∠FOE=2x,可知∠AOD=5x,∠AOD(5x)+∠BOD(70°)=∠AOB(120°),可算出x。
计算:
解:
(1)由已知条件和图中得知:
![]()
![]()
![]()
(2)
![]()
![]()
![]()
(3)存在。存在理由如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. 用A,B,C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25°,小红家在小明家正东,小红家在学校北偏东35°,则∠ACB等于()。
观察:注意审题,分清方向,明确方向角的概念,画出图形。
思考:根据观察画出图形:

从图中可知∠ACB与35°互为余角,所以∠ACB=55°。
2、相交线与平行线
①求角类题型
求角类题型较多,如顶角、邻补角的识别和性质求角;利用垂直概念求角;利用同位角、内错角和同旁内角的识别求角;利用平行线的性质求角。
案例:
1. 如下图,DB//FG//EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数。

观察:注意审题,标记出已知条件。题中有三条平行线和已知条件∠ACE=36°,突破口应该在平行线的概念求角。
思考:利用FG//EC和∠ACE,可以知道∠GAC,已知∠PAG=12°,可求得∠PAC=∠PAG+∠GAC。已知AP平分∠BAC,那么∠BAP=∠PAC,即可求出∠BAG=∠BAP+∠PAG。
计算:
解:
![]()
![]()
![]()
![]()
![]()
![]()
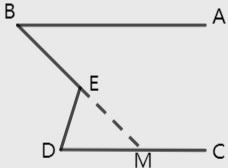
2. 如下图,AB//CD,试证明∠B+∠D=∠BED

观察:根据已知条件AB//BD,可以知道此题的突破口在平行线的性质上。
思考:根据观察我们可以确定突破口在平行线的性质上,但要应用平行线的性质,要使一条直线与两条平行线都相交,为了达到这个目的,我们要添加辅助线,构成一条直线与两条平行线相交。如下图:
计算:
证明:
延长线段BE,交直线CD于点M
![]()
![]()
![]()
![]()
![]()
![]()
总结:此类题型总结起来有六个模型:

②平行线的判定
案例:
1. 如下图,∠1=∠2=55°,∠3等于多少度?直线AB与CD平行吗?说明理由。

观察:可以观察到∠2和∠3为顶角,而∠1与∠2相等,那么∠1与∠3相等。
思考:根据同位角相等,则能判断两条直线平行。
计算:
解:
∠3=55°;
AB//CD,理由如下:
![]()
![]()
![]()
总结:此类型题证明的方法:
1.根据同旁内角、同位角或内错角,判断两直线平行;
2.利用平行线的判定定理结合平行公理的推论;
3.添加辅助线
四、总结


方法和技巧都不是独立的,而是要综合运用,并能举一反三,所以只是知道这些方法和技巧还不够,要针对这些方法多进行训练。
