有关平面直角坐标系内点的变换常见题型解题技巧
首先讲下几个关于坐标系的知识点:
1、坐标轴与象限:坐标轴实际就是两个垂直的数轴(x轴与y轴),两个数轴的原点重合形成交点(垂足),由于数轴有正负,两个数轴的正负互相组合就形成了四个象限;

2、对称点性质:关于x轴对称,横坐标不变,纵坐标变符号;关于y轴对称,纵坐标不变,横坐标变符号;关于原点对称,横竖坐标都变符号。
3、点到坐标轴的距离:到x轴的距离是纵坐标的绝对值;到y轴的距离是横坐标的绝对值;
4、坐标系内两点的中点公式:

这个公式十分重要,经常出现在考题中,不经常应用于求线段的中点来解决问题,还会以求一个点关于另一个点的对称点的形式出现。
现在咱们具几个例子来做做。
例题1:若点P(1-m,2+m)关于x轴对称的点的坐标在第一象限,则m的取值范围是 。
分析:求关于坐标轴的对称点,要清楚有一个坐标值是不变的,题目中求关于x轴的对称点,所以横坐标不变,纵坐标变符号。
解:P(1-m,2+m)关于x轴的对称点P′(1-m,-2-m)在第一象限
1-m>0且-2-m>0
得:m<-2
例题2:若a<0,点P(-a²-1,-a+3)关于原点的对称点为P1,则P1在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
分析:关于原点对称,横竖坐标都需要变符号,然后判断横竖坐标的取值范围,来确定其象限。
解:点P(-a²-1,-a+3)关于原点的对称点为P1(a²+1,a-3),a<0
∴a²+1>1,a-3<-3,得出P1在第四象限,所以选择D
例题3:如图,在平面直角坐标系中,线段OA与线段OA′关于直线l:y=x对称。已知点A的坐标为(2,1),则点A′的坐标为 。

分析:OA与OA′关于l:y=x对称,说明他们与l的夹角相等,过A做x轴的垂线,过A′做y轴的垂线,这样就形成两个全等的直角三角形,可以通过对应边相等求出A′的坐标。
解:过A做x轴的垂线垂足为B,过A′做y轴的垂线垂足为C
∵OA与OA′关于l:y=x对称
∴OA=OA′,不难求出∠BOA=∠COA′
∴△BOA≌△COA′
∴BA=CA′,BO=CO
∴A′(1,2)
例题4:如图,已知点A(0,2)、B(2 ,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA。

(1)当AB∥PQ时,点P的横坐标是 ;
(2)当BP∥QA时,点P的横坐标是 。
分析:抓住平行线的性质,线平行就会有角相等(还有同旁内角和是180°),画图分析此题会变得十分简单。
解:(1)如图,求出CP的长即可

(2)两种情况如图,可以直接求出点P的横坐标



例题5:将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是7/2 ,则点C的坐标是 。

分析:看到特殊四边形求顶点,就要想到特殊四边形的对角线平分这个性质,绝大多数的此类问题需要通过中点公式来解决问题。题中的A、O都是已知的,B点的纵坐标已知,这样可以求出C的纵坐标,也就是以OC为斜边与x轴构成的直角三角形的一条直角边已知,而OA与x轴构成的三角形与其相似,所以可以利用三角形相似来求C的横坐标。
解:连接AC、OB交于点F,则在矩形OABC中,F平分AC和OB,过A做AD⊥x于D,C做CE⊥x,于E,如图:

设点F(x0,y0),C(x,y),则:(7/2+0)/2=y0=(2+y),得:y=3/2
∵△OAD∽△COE,∴OD/AD=CE/OE,得:OE=3,x=3
∴C(3,3/2)
通过以上例题,你是否对坐标系内点的变换掌握了呢?用小作业来试试吧。
1、如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点

(Ⅰ)若点P的坐标为(1,1/4),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由。
2、如图,△ABC中,∠A=67.5°,BC=4,BE⊥CA于E,CF⊥AB于 F,D是BC的中点。以F为原点,FD所在直线为x轴构造平面直角坐标系,则点E的横坐标是?

----------------------------------------------------------------------------------------------------------------------------------
我们今天采用函数图象法秒解一道平面直角坐标系点坐标题目,例题本身比较简单,常规解法也不算太麻烦,因此秒解的意义只有一个,那就是“快!稳!”,题目如下:
无论m为何值,P(m-3,4-2m)不可能在第_________象限.
[常规思路解析]
①若点P在第一象限,则有m-3>0 且 4-2m>0,连立,m无解;
②若点P在第二象限,则有m-3<0 且 4-m>0,连立解得m<3;
③若点P在第三象限,则有m-3<0 且 4-2m<0,连立解得2<m<3;
④若点P在第四象限,则有m-3>0 且 4-2m<0,连立解得m>3;
∴无论m为何值,P(m-3,4-2m)不可能在第一象限。
没毛病,根据已知的坐标代数式,按照四个象限分情况讨论,连立解不等式组,即可得到正确答案。这也是我在网上找到的本题的唯一解法。But... ...对于本题,秒答君想说,换个思路,海阔天空,请看秒答解析。
[解析]
1. 有题可知,点P的横、纵坐标均为m的函数,如果我们连立两个函数式,则可以求得点P的纵横坐标之间的关系。
也就是说,设P点坐标为(x,y),由题意,有
x=m-3,y=4-2m,连立消m,可得
y=-2x-2。
2. 可见,无论m为何值,点P都要满足这个关系式。即点P一定在直线
y=-2x-2上,
这是一条斜率为负、截距为负的直线,过二、三、四象限。因此,点P不可能在第一象限。
本题采用函数图象法比常规解法简便、快速、直观,有且具有更广泛的适应性,比如将此题变形,问点P能否在平面坐标系某一区域内,前面常规解法就更加麻烦,而函数图象法同样适用。
本讲提示:函数图象法原理稍微有点绕,请仔细体会。
------------------------------------------------------------------------------------------------------------------------
函数图象法,秒解平面直角坐标系-点坐标题
我们今天采用函数图象法秒解一道平面直角坐标系点坐标题目,例题本身比较简单,常规解法也不算太麻烦,因此秒解的意义只有一个,那就是“快!稳!”,题目如下:
无论m为何值,P(m-3,4-2m)不可能在第_________象限。

题目
[常规思路解析]
①若点P在第一象限,则有m-3>0 且 4-2m>0,连立,m无解;
②若点P在第二象限,则有m-3<0 且 4-m>0,连立解得m<3;
③若点P在第三象限,则有m-3<0 且 4-2m<0,连立解得2<m<3;
④若点P在第四象限,则有m-3>0 且 4-2m<0,连立解得m>3;
∴无论m为何值,P(m-3,4-2m)不可能在第一象限。
[解析]
1. 由题可知,点P的横、纵坐标均为m的函数,如果我们连立两个函数式,则可以求得点P的纵横坐标之间的关系。
也就是说,设P点坐标为(x,y),由题意,有
x=m-3,y=4-2m,连立消m,可得 y=-2x-2。
2. 可见,无论m为何值,点P都要满足这个关系式。即点P一定在直线 y=-2x-2上,
这是一条斜率为负、截距为负的直线,过二、三、四象限。因此,点P不可能在第一象限。


------------------------------------------------------------------------------------------------------------------------
初中平面直角坐标系中点到直线的距离求解方法
问题引入:在平面直角坐标系中,已知直线的位置及任意点的坐标,在初中阶段没有学习点到直线的距离公式时,探究如何求点到直线的距离。
具体方法:
方法一:平行线
方法二:垂直交点法
方法三:面积法
方法四:相似法
作用:常见于二次函数综合题中,求抛物线或双曲线上的动点P到直线的最值问题.如图

小结:线在曲线外部时,动点到线AB的距离有最小值;面积最小.

小结:线在曲线内部时,动点在交点范围内运动到线AB的距离有最大值;面积最大.
例题:已知直线的解析式为y=2x+6,点P的坐标为(2,2),求点P到直线的距离.

方法一:平行线法
思想方法:通过作平行线构造直角三角形,利用解直角三角形求点到直线的距离。
①作平行线(求两平行线间的距离)
②解直角三角形



方法二:垂线交点法
思想方法:通过作垂线求交点坐标,利用两点间的距离公式。
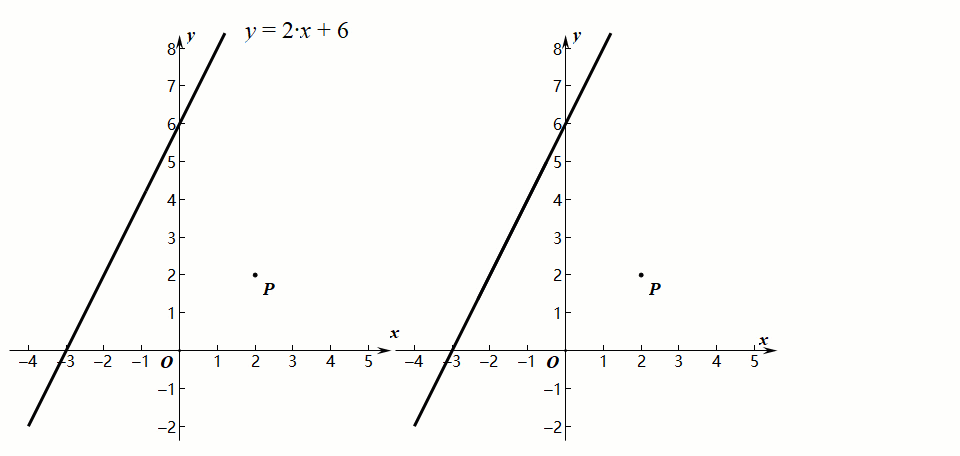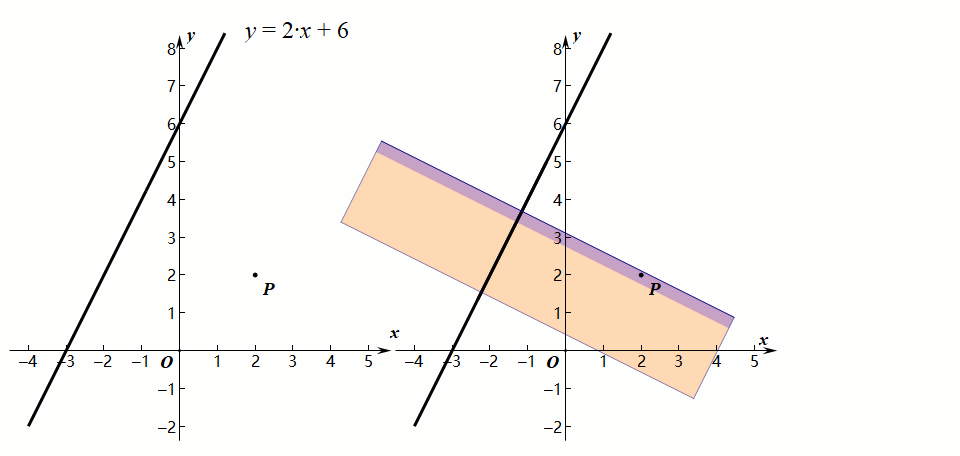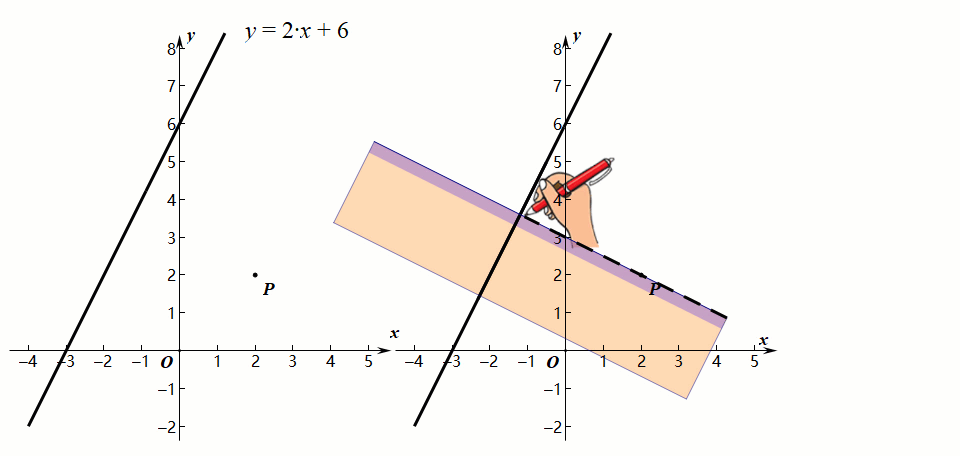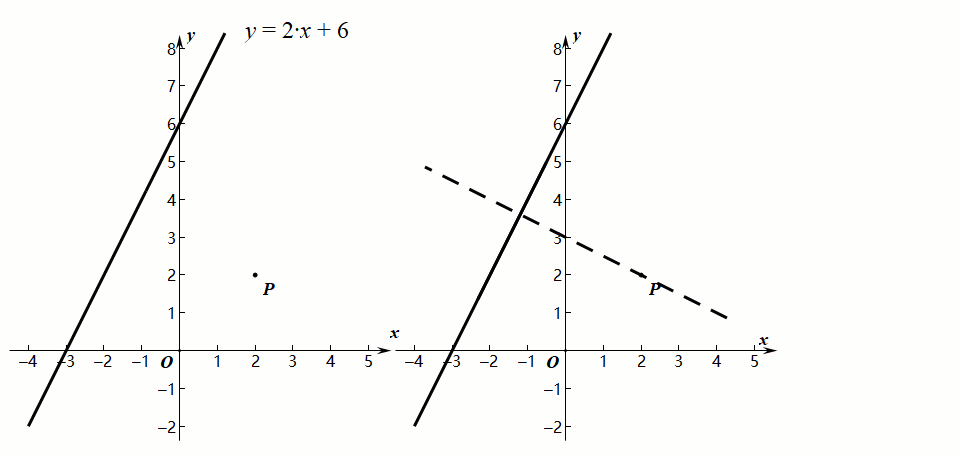
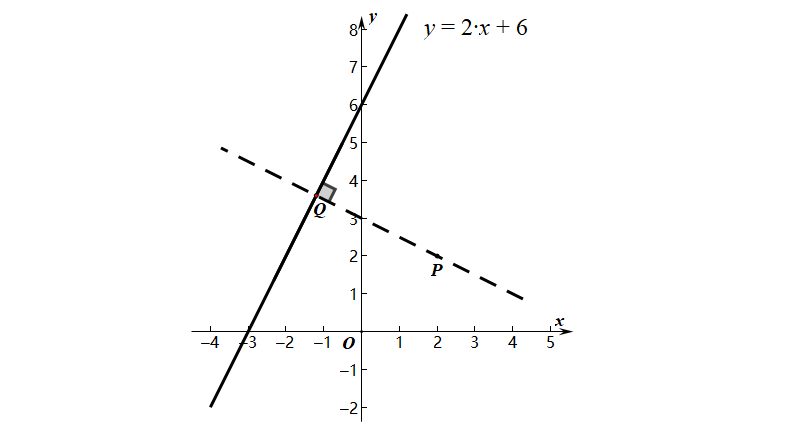

方法三:面积法
思想方法:一般利用割补法(铅锤法常用)求△ABP的面积,再求出AB的长度,则AB边上的高PE可求.

方法四:相似法

